Quantum Numbers and Angular Momentum So a larger value of l means more angular momentum? That's right. If you really want to know the exact mathematical relationship between l and angular momentum, click on the advanced button. We've seen that states with higher values of l have more energy--p states have a higher energy than s states, and so on. I'm not quite sure why more angular momentum means more energy. Well, the larger its angular momentum, the farther from the nucleus an electron tends to be. That makes sense--the same thing is true for planets orbiting the sun, right? I know electrons don't orbit exactly, but... No, your intuition is good. It's difficult to see how the idea of angular momentum even applies to something that's just existing amorphously in a cloud, and yet it has to; the theory simply won't work without it. To have any picture of what's happening, we have to fall back on that same old wrong-but-useful orbiting idea. Now, suppose you're an electron with lots of angular momentum, floating out there beyond your less well-endowed friends. Any electrons between you and the nucleus are "screening" you from the full effect of the central positive charge. Think about boron, for example; the two innermost electrons feel all five protons pulling them in, but the highest electron "sees" four electrons between it and the five protons, so the total charge it feels is hardly more than that of one proton. And the less strongly it's pulled in, the less energy it needs to escape --so that's why a larger l means a higher energy. What about that third quantum number you mentioned? Is m also related to angular momentum? 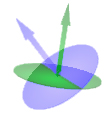Yes; m refers, loosely, to the direction of the angular momentum vector. (Want an exact formula?) As you might expect, m doesn't affect the electron's energy, but it does affect the probability cloud.

>