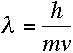
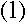
Circular Waves and the Bohr Model De Broglie proposed that every particle has a wavelength equal to Planck's constant divided by its momentum. Thus, an electron with mass m and speed v would have a wavelength of Now, if the wave has to fit into a circular "orbit" of radius r, the circumference of that circle must be exactly as long as a whole number of wavelengths: where n is a positive integer. 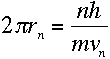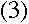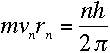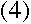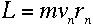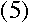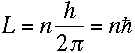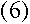Plugging in the wavelength from equation (1), we get or But we know that for a circular orbit, Thus, if we assume the electron is a wave with its wavelength given by de Broglie's formula, then we automatically get Bohr's constraint on its angular momentum: The integer n, as we've noted earlier, corresponds to the energy level; thus, for example, an electron in the third energy level would have three wavelengths around its orbit, and so on.

>