Vibrating Charges Revisited
 I'm not sure I understand what you mean by "vibrating." How does the Bohr model for an atom
relate to the ideas we were talking about earlier? You compared "vibrating charges" to
oscillating springs; how does that fit in with Bohr's idea of jumps between orbits?
I'm not sure I understand what you mean by "vibrating." How does the Bohr model for an atom
relate to the ideas we were talking about earlier? You compared "vibrating charges" to
oscillating springs; how does that fit in with Bohr's idea of jumps between orbits?
 Let's step back from the Bohr model for a moment and look at an earlier model for the atom--
don't worry, you've seen this before. Remember when you were playing around with
orbits, and I said you'd created a simplified
version of an atom?
Let's step back from the Bohr model for a moment and look at an earlier model for the atom--
don't worry, you've seen this before. Remember when you were playing around with
orbits, and I said you'd created a simplified
version of an atom?
 That was just an electron orbiting around a proton.
That was just an electron orbiting around a proton.
|
 So does the Rutherford model relate to the "charge on a spring" idea?
So does the Rutherford model relate to the "charge on a spring" idea?
 It certainly does. An electron orbiting a nucleus moves periodically, just like the charge on
a spring you saw earlier. Both are undergoing simple harmonic motion; if you project the
orbiting electron's motion into one dimension, it will look just like a mass oscillating on a
spring.
It certainly does. An electron orbiting a nucleus moves periodically, just like the charge on
a spring you saw earlier. Both are undergoing simple harmonic motion; if you project the
orbiting electron's motion into one dimension, it will look just like a mass oscillating on a
spring.
|
 So if an electron is orbiting, you could say it's "vibrating" at a certain frequency, which
depends on the radius of its orbit. That makes sense. But when we discussed the "charge on a
spring," you said that if an electron vibrates at a particular frequency, it must produce
electromagnetic radiation at that same frequency. So if you had, say, a hydrogen atom with an
electron orbiting at some fixed radius, it would always be giving off radiation--that
can't be right.
So if an electron is orbiting, you could say it's "vibrating" at a certain frequency, which
depends on the radius of its orbit. That makes sense. But when we discussed the "charge on a
spring," you said that if an electron vibrates at a particular frequency, it must produce
electromagnetic radiation at that same frequency. So if you had, say, a hydrogen atom with an
electron orbiting at some fixed radius, it would always be giving off radiation--that
can't be right.
 Yes, Rutherford's picture of the atom has a couple of fundamental problems. First of all,
there's no apparent reason why an electron's orbit couldn't have just any old radius, and thus
any old frequency. That flatly contradicts the experimental evidence of
spectral lines.
Yes, Rutherford's picture of the atom has a couple of fundamental problems. First of all,
there's no apparent reason why an electron's orbit couldn't have just any old radius, and thus
any old frequency. That flatly contradicts the experimental evidence of
spectral lines.
 Well, isn't that why Bohr came up with the idea of electrons' being restricted to certain
special orbits?
Well, isn't that why Bohr came up with the idea of electrons' being restricted to certain
special orbits?
 Yes, that's a partial solution. Let's assume that an electron's orbit, for some mysterious
reason, can only have certain discrete radii. Now suppose that an electron is happily
cruising along in one of these legal orbits. As you've said, the electron is "vibrating," so
it ought to be producing radiation. So, let's say our electron emits an electromagnetic wave
of the proper frequency. That's all well and good until you start to think about the
energy contained in that wave...
Yes, that's a partial solution. Let's assume that an electron's orbit, for some mysterious
reason, can only have certain discrete radii. Now suppose that an electron is happily
cruising along in one of these legal orbits. As you've said, the electron is "vibrating," so
it ought to be producing radiation. So, let's say our electron emits an electromagnetic wave
of the proper frequency. That's all well and good until you start to think about the
energy contained in that wave...
 Waves have energy?
Waves have energy?
 If the wave made that second charge move, then it must have carried energy from the + charge
to the - charge.
If the wave made that second charge move, then it must have carried energy from the + charge
to the - charge.
 So the moving wave contains energy...and energy is conserved.
So the moving wave contains energy...and energy is conserved.
|
 Then in order to emit the wave, the electron has to give up some of its own energy.
Then in order to emit the wave, the electron has to give up some of its own energy.
|
 Exactly; the electron would have to slow down, which would decrease its kinetic energy.
But if it did that, it wouldn't be able to remain at a fixed radius; it would be pulled in
closer to the nucleus. (Note: this actually does happen for macroscopic objects in
orbit; stars in a binary system, for example, spiral slowly in toward one another,
because as they orbit they give off energy in the form of gravitational waves.)
Exactly; the electron would have to slow down, which would decrease its kinetic energy.
But if it did that, it wouldn't be able to remain at a fixed radius; it would be pulled in
closer to the nucleus. (Note: this actually does happen for macroscopic objects in
orbit; stars in a binary system, for example, spiral slowly in toward one another,
because as they orbit they give off energy in the form of gravitational waves.)
|
 |
 And meanwhile the electron would still be wiggling, so it would give off another wave (at a
different frequency), which would make its orbit decay even more...when would this
ever end?
And meanwhile the electron would still be wiggling, so it would give off another wave (at a
different frequency), which would make its orbit decay even more...when would this
ever end?
 It wouldn't. The electron would keep right on spiraling inward until it crashed into the
nucleus, at which point there would be no more atom. So if this classical picture were
correct, atoms would be highly unstable, and nothing made of atoms could possibly exist
for more than a fraction of a second. You and I couldn't be having this conversation if
it weren't for quantum mechanics.
It wouldn't. The electron would keep right on spiraling inward until it crashed into the
nucleus, at which point there would be no more atom. So if this classical picture were
correct, atoms would be highly unstable, and nothing made of atoms could possibly exist
for more than a fraction of a second. You and I couldn't be having this conversation if
it weren't for quantum mechanics.
 Okay, so it sounds like you're saying that the Bohr model and the Rutherford model
actually have nothing to do with each other. Rutherford's classical picture was just
completely wrong, so Bohr had to come up with something entirely new.
Okay, so it sounds like you're saying that the Bohr model and the Rutherford model
actually have nothing to do with each other. Rutherford's classical picture was just
completely wrong, so Bohr had to come up with something entirely new.
 Well...yes and no. This classical model is inaccurate, but there are cases in
which the correspondence principle applies. Just as Newtonian mechanics is a good
approximation to relativity at low velocities, Rutherford's model is a good approximation
to the Bohr model for closely packed energy levels.
Well...yes and no. This classical model is inaccurate, but there are cases in
which the correspondence principle applies. Just as Newtonian mechanics is a good
approximation to relativity at low velocities, Rutherford's model is a good approximation
to the Bohr model for closely packed energy levels.




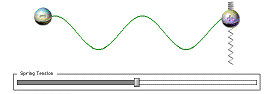
 Take another look at that vibrating charge. Notice how when the wave reaches the negative
charge on the left, that charge starts bouncing up and down? The original + charge never
touched that negative charge; only the wave did.
Take another look at that vibrating charge. Notice how when the wave reaches the negative
charge on the left, that charge starts bouncing up and down? The original + charge never
touched that negative charge; only the wave did.