Speed of Light Kyla, do you remember how the wavelength of the electromagnetic wave became shorter when the charge was vibrating faster? Right, but the wave seemed to move with the same speed whether the vibration was fast or slow. Only the wavelength changed when the oscillations became faster. Yes, all electromagnetic radiation -- from radio waves to x-rays -- travel at the speed of light. In empty space this speed is approximately 300,000 kilometers per second! We can even predict the wavelength of an electromagnetic wave if we know the time it takes for the charge to oscillate once, returning to its original location. This time is called the "period", T, of the wave. By multiplying the period with the speed of light (c), we can determine the wavelength of any wave. Oh, I get it! One gray dot takes a time "T" to go up and down, completing one cycle of the wave. The other dot stays on the crest of the wave and moves a distance, "d", equal to one wavelength. But I have a lot of questions: Is the period "T" for the wave the same as the period for the charge? Yes. Why is d/T equal to the speed of the wave? Well, the gray dot that moves a distance "d" has the same speed as the wave because it is carried along with the wave. Since the time it takes to move that distance is equal to "T," the speed is "d/T". That is just like a car moving 100 miles in two hours at constant speed. The car must be traveling 100/2=50 miles per hour. But how do we know that the speed of light is always almost 300,000 kilometers per second? Good question. It's just a fact of nature that the speed of electromagnetic radiation moving through empty space always has the same value. What is meant by the "frequency" of the wave? The frequency, "f," is the number of completed periods in one second. If the period is 1/2 second, the frequency will be two wavelengths per second (1/2 second for one wavelength, so two wavelengths in one second). 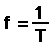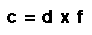In general, So our formula can also be written as The speed of the wave is equal to the wavelength times the frequency. Oh, I see; now we can figure out the wavelength of any wave if we know the frequency, and vice versa. 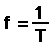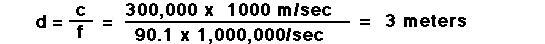My favorite radio station is at 90.1 MHz, so the wavelength of those radio waves must be , or That's about 10 feet from peak to peak!

>