Zakład Fizyki Magnetyków

Magnetyczne uporządkowanie w ultracienkich warstwach

Omawiane w niniejszym opracowaniu wyniki badań zostały uzyskane w Zakładzie Fizyki Magnetyków UWB przy wsparciu finansowym Komitetu Badań Naukowych, w ramach ścisłej współpracy z ośrodkami naukowymi krajowymi (np. Instytut Fizyki PAN w Warszawie, Zakład Fizyki Ciała Stałego AGH w Krakowie oraz Instytut Katalizy i Fizykochemii Powierzchni PAN w Krakowie) i zagranicznymi (np. Laboratoire de Physique des Solides, Universite Paris-Sud & CNRS, Orsay,Francja,National University of Donetsk, Ukraina, Institute of Physics ASCR, Praga, Czechy). Wyniki badań były publikowane w pracach http://physics.uwb.edu.pl/zfmag/index.php?tr=Publikacje oraz prezentowane na wielu konferencjach naukowych, ostatnio m.in.: 47th Magnetism and Magnetic Materials Conference , Tampa, Floryda 2002, USA; 7th Korean-Polish Joint Seminar on Physical Properties of Magnetic Materials , Warsaw 2002, XVIII International Colloquium on Magnetic Films and Surfaces , Madrid, Spain 22-25 VIII 2003, International Conference on Magnetism, Roma, Italy 28 VII- 1 VIII 2003, XXVII Zjazd Fizyków Polskich, Gdańsk 15-19 IX 2003, European Materials Research Society Fall Meeting, Warszawa 15-19 IX 2003.

Niniejsze opracowanie zostało wykonane w oparciu o tekst wykładu
dr M. Kisielewskiego na XXVII Zjezdzie Fizyków Polskich.

W przeciwieństwie do dobrze już poznanego, opisywanego w podręcznikach magnetyzmu materiałów litych i materiałów o rozmiarach mikrometrowych [1],uporządkowanie magnetyczne ultracienkich warstw, czyli warstw o grubości kilku odległości między-atomowych (a więc rzędu 1 nm), nadal kryje w sobie jeszcze wiele tajemnic. Dzięki temu obiekty te od wielu już lat cieszą się ogromnym, niesłabnącym zainteresowaniem [2], dodatkowo stymulowanym przez imponujący rozwój technologii wzrostu warstw, umożliwiający obecnie wytwarzanie doskonałych jakościowo materiałów, konstruowanych na zasadzie kolejnego osadzania poszczególnych warstw atomowych według zadanej z góry kolejności [3] oraz przez silną presję związaną z nadziejami na ich zastosowanie techniczne (np. do zapisu informacji). Ogromne znaczenie ma też walorpoznawczy układów o obniżonej wymiarowości, które obfitują w wiele ciekawychefektów, jak chociażby zjawisko gigantycznego magneto-oporu (GMR) [4], które zrobiło w drugiej połowie lat dziewięćdziesiątych ubiegłego wieku zawrotą "karierę" i które już wkrótce po odkryciu zaczęto stosować w technice komputerowej (w nowego typu dyskowych głowicach odczytujących) czy w motoryzacji (w czujnikach obrotu w układach ABS).

Typowym zjawiskiem obserwowanym w ultracienkich warstwach magnetycznych jest silna zależność anizotropii magnetycznej od grubości warstwy. Mechanizm tej zależności związany jest ze znaczącym wzrostem anizotropii powierzchniowej przy małych grubościach (zazwyczaj mniejszych od 2nm) w stosunku do anizotropii objętościowej. Energia anizotropii magnetycznej może być opisana dla takich obiektów standartowym wzorem:

E_a=K_1effsin²θ+K₂sin⁴θ= [K_1V-2πM_S²+(K_1Sd+K_1Sg)/d]sin²θ+ K₂sin⁴θ, (1)

w którym K_1eff jest efektywną stałą anizotropii, K_1V jest stałą anizotropii objętościowej, K_1Sd i K_1Sg jest anizotropią powierzchniową wnoszoną odpowiednio przez dolną i górną powierzchnię graniczną warstwy magnetycznej, M_S jest namagnesowaniem nasycenia, a θ jest kątem pomiędzy namagnesowaniem i normalną do powierzchni próbki. Konsekwencją tej zależności jest możliwość zmiany znaku K_1eff z dodatniego na ujemny w miarę wzrostu grubości i wystąpienie reorientacyjnego przejścia fazowego, w którym namagnesowanie zmienia orientację od orientacji prostopadłej do warstwy do orientacji równoległej do warstwy.

Od połowy lat dziewięćdziesiątych ubiegłego wieku prowadzono w wielu ośrodkach intensywne badania in-situ (czyli w warunkach "kosmicznej", ultra-wysokiej próżni), które wykazały silną zależność członu K_1Sg od rodzaju materiału pokrywającego warstwę magnetyczną [5-10].

Cel badań

Naszym celem było wykonanie kompleksowych badań ex-situ wpływu grubości niemagnetycznej warstwy pokrywającej na uporządkowanie magnetyczne ultracienkiej warstwy kobaltu [11]. Drugim celem było zbadanie rozmiarów domen magnetycznych w możliwie szerokim zakresie: zarówno daleko od przejścia fazowego jak też i w jego pobliżu [12], bowiem można oczekiwać wystąpienia gigantycznych zmian tych rozmiarów.

Wpływ warstwy pokrywającej na właściwości magnetyczne ultrasienkiej warstwy

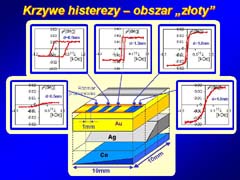
Oryginalne struktury podwójnych klinów [11] do badania wpływu struktury warstwy pokrywającej na uporządkowanie magnetyczne kobaltu wykonano w Instytucie Fizyki PAN w Warszawie metodą epitaksji z wiązak molekularnych -MBE (problematyka optymalizacji wzrostu warstw poruszana była w pracach [13] i [14]). Próbki miały następującą budowę (Rys.1): na szafirowej podkładce, wzbogaconej o dodatkowe warstwy buforowe molibdenu i złota (zapewniające optymalny wzrost warstwy magnetycznej), osadzono klin kobaltu, a następnie, w pewnej odległości od krawędzi próbki, klin srebra, przechodzący w płaską warstwę srebra, w sposób pokazany na Rys.1, i całość przykryto warstwą złota. Uzyskano tym sposobem w środkowej części próbki przestrzenną modulację zarówno grubości warstwy kobaltu d jak i składu chemicznego warstwy pokrywającej, a przy dwóch przeciwległych brzegach próbki dwa obszary "referencyjne", w których klin kobaltu przykryty był albo tylko stosunkowo grubą płaską warstwą Au ( tzw. obszar "złoty") albo stosunkowo grubą płaską warstwą Ag i potem Au (ten obszar można nazwać obszarem "srebrnym", ponieważ kobalt ze względu na odległość "wyczuwa"tutaj praktycznie tylko obecność Ag). Dzięki temu można było zbadać wpływ na właściwości magnetyczne kobaltu najpierw oddzielnie złota i oddzielnie srebra, a następnie obu tych metali razem.

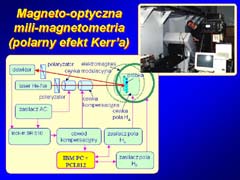
Przy pomocy magnetooptycznego mili-marnetometru, przedstawionego schematycznie na Rys.2, analizującego na bazie efektu Kerra sygnał optyczny z wycinka próbki o rozmiarach rzędu milimetra, zmierzono [11] dla obu obszarów referencyjnych krzywe histerezy φ(H_⊥) , czyli zależności kątem skręcenia Kerra φ od pola skierowanego prostopadle do powierzchni próbki H_⊥. Przykładowe krzywe histerezy pokazane są na Rys.3.


Rys.1	Rys.2	Rys.3

W oparciu o analizę krzywych histerezy, wyznaczono zależność pola koercji H_C od d, zależność maksymalnej wartości kąta skręcenia Kerra φ_max od d oraz zależność unormowanego namagnesowania remanencyjnego m_R =φ_(H=0)/φ_max od d dla obu obszarów referencyjnych.

W oparciu o analizę krzywych histerezy, zmierzonych po przyłożeniu dodatkowego stałego pola zorientowanego równolegle do płaszczyzny próbki, wyznaczono [11] zależności stałych anizotropii jednoosiowej od grubości d w obszarze "złotym" i "srebrnym" - patrz Rys. 5. Linie ciągłe K_1eff(d) wyliczono ze wzoru (1) z parametrami uzyskanymi z dopasowania: K_1s=(0.57ą0.03)erg/cm², K_1v=(6.3ą0.4)Merg/cm³ dla obszaru "złotego" i K_1s = (0.42ą0.04) erg/cm², K_1v=(6.2ą0.6)Merg/cm³ dla obszaru "srebrnego". Na Rys.5 przedstawione są także diagramy stanu magnetycznego, skonstruowane dla obu obszarów z uwzględnieniem poziomych linii kreskowanych, reprezentujących średnie wartości -2K₂. Z Rys.5 wynika, że grubość krytyczna reorientacyjnego przejścia fazowego dla obszaru "srebrnego" (d₁^Ag) jest o ponad 0.5nm mniejsza od grubości krytycznej dla obszaru "złotego" (d1Au). W obu przypadkach jest to przejście fazowe drugiego rodzaju, w którym, wraz ze wzrostem d, namagnesowanie zmienia swój kierunek od orientacji prostopadłej do powierzchni warstwy (łatwa oś) poprzez orientację nachyloną (łatwy stożek) do orientacji równoległej do płaszczyzny warstwy (łatwa płaszczyzna przy d > d₂).


Rys.4	Rys.5

Analizę stanu magnetycznego zasadniczego dwu-klinowego obszaru próbki przeprowadzono z większą rozdzielczością przestrzenną, przy pomocy polaryzacyjnego mikroskopu Kerra, wyposażonego w sprzężoną z komputerem kamerę CCD o wysokiej czułości (schemat zastosowanego mikromagnetometru magnetooptycznego przedstawiony jest na Rys. 6). Do analizy zastosowano specjalnie opracowaną w tym celu metodę rejestracji obrazów remanencyjnych (Rys.7), polegającą na rejestracji kolejno dwóch obrazów próbki przemagnesowanej polem H_⊥ skierowanym raz "do dołu" (H_⊥<0) a raz "do góry" (H_⊥>0), i na różnicowaniu tych obrazów. Stopień jasności danego punktu na obrazie różnicowym jest proporcjonalny do iloczynu φ i m_R w tym punkcie.


Rys.6	Rys.7	Rys.8

Mapa remanencyjna całej próbki (10x10mm²), uzyskana po zastosowaniu tej metody, przedstawiona jest na Rys.8 (pole H_⊥ ( skierowane "do góry" wynosiło w tym przypadku 345 Oe). Jasny obszar, widoczny w środkowej części, oznacza stan z prostokątną pętlą histerezy (patrz histereza dla d=1.3nm na Rys.3), a ciemne obszary po lewej i po prawej stronie oznaczają odpowiednio: (i) stan superparamagnetyczny lub ferromagnetyczny o zaniedbywalnej remanencji, oraz (ii) stan z namagnesowaniem w płaszczyźnie. Na rysunku schematycznie zaznaczono stan magnetyczny środkowego obszaru jasnego oraz ciemnego po prawej stronie, a także rozkład grubości Co i Ag, odpowiednio wzdłuż osi "x" i "y". Ciemny obszar o podłużnym, spiczasto zakończonym kształcie znajdujący się na dole w środkowej części mapy, wskazuje taki rejon z prostokątną pętlą histerezy, którego zastosowane podczas rejestracji pole (345 Oe) nie było w stanie przemagnesowć (patrz także Rys.9). Granica pomiędzy obszarem jasnym i ciemnym prawym oznacza linię przejścia fazowego. Linia ta wykazuje silne zakrzywienie w obszarze zmienności grubości srebra i przechodzi w odcinki proste w obszarach referencyjnych. Właśnie ta zakrzywiona część jest najbardziej interesująca, niesie bowiem informację o dynamice wpływu grubości srebra na magnetyczną anizotropię. Zakładając eksponencjalny ( exp(-h/h^*) ) charakter przestrzennej zmienności kształtu tej linii w funkcji grubości srebra h, można oszacować grubość charakterystyczną h^*≈1nm (patrz czerwone linie ciągłe na Rys.8, opisujące przestrzenny charakter przejścia fazowego dla kilku różnych h^*).

Jednocześnie warto zwrócić uwagę na nowy obiekt magnetyczny, mianowicie 90-stopniowej ścianę, którą można nazwać ścianą "chemiczną". cianę tę napotyka się wędrując wzdłuż kierunku wzrostu grubości srebra h (a więc wzdłuż osi "y" na Rys.8) przy pewnej ustalonej grubości kobaltu d z przedziału od ok. 1.3 nm do 1.8 nm w chwili mijania linii przejścia fazowego. Szerokość tej ściany może być zmieniana w zakresie wielu rzędów wielkości poprzez odpowiedni dobór d i gradientu grubości srebra. W sąsiedztwie grubości krytycznej d₁^Au już nawet ułamek monowarstwy Ag jest w stanie dokonać reorientacji namagnesowania kobaltu!

Tak więc w próbce wytworzył się przestrzenny rozkład anizotropii, związany ze zmianą d oraz ze strukturą warstwy pokrywającej. Powstał także przestrzenny rozkład koercji. Rozkład ten można badać poprzez analizę kształtu struktury domenowej pojawiającej się po przyłożeniu impulsu pola magnetycznego np. H_⊥>0 do próbki, która wcześniej była nasycona przy pomocy pola H_⊥<0. Stosując tę procedurę, obserwuje się wraz ze wzrostem wartości impulsu H_⊥ >0 przesuwanie się granicy obszaru przemagnesowanego (czyli przesuwanie tak zwanej "ściany koercji") od obszarów o małej wartości pola koercji H_C w stronę obszarów o dużej wartości H_C - patrz Rys.9, na którym liniami kropkowanymi zaznaczono ściany koercji dla kilku wybranych wartości pól H_⊥. Charakter przestrzennych zmian kształtu ściany koercji w funkcji h jest analogiczny do zmian anizotropii. Przykładowe czerwone krzywe ciagłe widoczne na Rys.9, zostały obliczone dla charakterystycznej grubości h_C^*=0.8nm. Zakładając eksponencjalny charakter przestrzennej zależności H_C od h, oraz uwzględniając zmierzone wcześniej zależności H_C(d) dla obszarów referencyjnych (Rys.4) można dokonać rekonstrukcji przestrzennego rozkładu H_C dla całej próbki - patrz trójwymiarowy diagram na Rys.9.


Rys.9	Rys.10

Analizując powiększone obrazy ściany koercji dla różnych d można stwierdzić istotne zmiany charakteru struktury domenowej. Wraz ze wzrostem d w pobliżu przejścia fazowego struktura ta staje się coraz bardziej fraktalna i przemagnesowanie następuje poprzez rosnącą liczbę centrów nukleacji. Jest to widoczne na Rys.10 [15] na przykładowych remanencyjnych obrazach struktury domenowej (0.44x0.35mm²), zarejestrowanych w obszarze "złotym" (na każdym z obrazków struktury domnowej podana jest wartość pola magnetycznego w Oe; punkty białe i czarne oznaczają namagnesowanie odpowiednio "do góry" i "do dołu"). W bezpośrednim sąsiedztwie przejścia fazowego rozmiary struktury stają się na tyle małe, że nie można już jej obserwować metodami optycznymi.

Rozmiary magnetycznych struktur domenowych

Wgląd w uporządkowanie magnetyczne w okolicach przejścia fazowego umożliwiła kompleksowa analiza ewolucji rozkładów namagnesowania, obejmująca zarówno rozważania teoretyczne jak i symulacje mikromagnetyczne [12,20]. Analiza ta została wykonana dla przejścia fazowego indukowanego bądź zmianą K_1eff bądź polem magnetycznym przyłożonym w płaszczyźnie warstwy H_II (dla przypadku warstwy o anizotropii typu łatwa oś) patrz Rys.11. Wykazała ona, że odmagnesowanie ma bardzo istotny wpływ na uporządkowanie magnetyczne w pobliżu przejścia i że rozmiary struktury domenowej mogą się zmieniać o wiele rzędów wielkości: od zaledwie kilkudziesięciu nanometrów - w pobliżu przejścia, do dziesiątków metrów (praktycznie nieskończoność) - daleko od przejścia fazowego. Drastycznie zmienia się też przy tym rozkład namagnesowania: o ile daleko od przejścia fazowego szerokość ściany domenowej jest zaniedbywalnie mała w stosunku do rozmiarów domen, to o tyle w pobliżu przejścia szerokość ściany staję się porównywalna z rozmiarami domen co prowadzi do pojawienia się tzw. sinusoidalno-podobnej struktury domenowej (patrz Rys.12) o periodzie określonym przez stosunek energii wymiany do energii odmagnesowania i wynoszącym 8πl_ex²/d (gdzie l_ex jest tzw. długością wymiany; w przypadku kobaltu równą 3.2nm). Możliwość sterowania rozmiarami domen przy pomocy pola H_II wydaje się szczególnie ciekawa, pozwala bowiem uzyskiwać ogromne zmiany periodu w sposób odtwarzalny i to na dodatek w jednej i tej samej próbce. Zależności rozmiarów domen od magnetycznej historii została eksperymentalna stwierdzona [16] dla płaskiej warstwy kobaltu szafir/Mo(20nm)/Au(20nm)/Co(d=1nm)/Au(8nm) i jest zilustrowana na Rys.13. Na Rys.13 po prawej stronie widoczny jest obraz remanencyjny (2x2mm ²) z białymi domenami o rozmiarach rzędu jednego milimetra, które zostały zarejestrowane przy pomocy mikroskopu Kerra, po uprzednim nasyceniu próbki przy pomocy pola H_⊥>0, preferującego domeny "czarne" i po przyłożeniu krótkiego impulsu pola H_⊥>0 o odpowiedniej wartości, preferującego domeny "białe". O rozmiarach domen decydują w tym przypadku głównie defekty, a nie magnetostatyka. Natomiast na Rys.13 po lewej stronie widoczny jest obraz struktury (20 μm x 20 μm) z domenami o rozmiarach sub-mikronowych, uzyskanymi poprzez chwilowe zadziałanie pola H_II nasycającego próbkę. Obraz ten został zarejestrowany przy pomocy mikroskopu sił magnetycznych (MFM). Domeny wytworzone w pobliżu przejścia fazowego indukowanego polem H_II zostały w chwili wyłączania pola "zamrożone" przez koercję próbki.


Rys.11	Rys.12	Rys.13

Podsumowanie

Reasumując należy stwierdzić, że uporządkowanie magnetyczne ultracienkiej warstwy kobaltu bardzo silnie zależy od struktury warstwy pokrywającej. Otwiera to nowe możliwości badawcze i stwarza szansę na nowe zastosowania. Narzucającym się wprost zastosowaniem jest np. bardzo prosta metoda zadawania przestrzennego rozkładu magnetycznych właściwości próbki poprzez wprowadzenie do warstwy pokrywającej matrycy wysepek z innego materiału (tzw. magnetyczny patterning). Podobny skutek osiągano uprzednio w sposób daleko bardziej skomplikowany np. poprzez implantację jonów [17] czy też poprzez krystaliczno-polikrystaliczną modulację powierzchni warstwy buforowej [18].

Rys.14

Możliwość "manipulowania" rozmiarami domen magnetycznych w szerokim zakresie w ultracienkich warstwach (Rys.14) przy pomocy czy to pola H_II czy to anizotropii, otwiera nowe kierunki badań magnetycznych w skali sub-mikronowej. Bardzo ciekawe możliwości uzyskiwania zupełnie innych rozkładów namagnesowania pojawiają się w przypadku dalszego obniżania wymiarowości magnetyka (np. ograniczenie rozmiarów ultracienkiej warstwy w płaszczyźnie prowadzi do pojawienia się struktury wirowej, tzw. worteksów [19]).

Badania ultracienkich warstw prowadzone są przy wsparciu finansowym Komitetu Badań naukowych (Granty Nr. 4 T11B 006 24 oraz 4 T08A 025 23).

Literatura:

[1] A.Hubert and R.Schäfer, Magnetic Domains., Springer, Berlin (1998).

[2] Ultrathin Magnetic structures edited by B.Heinrich and J.A.C.Bland, Springer, Berlin, 1994.

[3] M.A.Herman, H.Sitter, Molecular Beam Epitaxy - Fundamentals and Current Status, wyd.2 (Springer-Verlag, Berlin, Heidelberg 1996)

[4] J.Shen, J.Kirschner, Surf. Sci. 500, 300 (2002)

[5] W.Weber, C.H.Back, A.Bischof, D.Pescia, and R.Allenspach, Nature, (London) 374, 788 (1995).

[6] S.Hope, E.Gu, B.Choi, J.C.Bland, Phys. Rev. Lett. 80, 1750 (1998).

[7] P.Beauvillain, A.Bounouh, C.Chappert, R.Megy, S.Ould-Mahfoud, J.P.Renard, P.Veillet, D.Weller, J.Corno, J.Appl.Phys. 76, 6078(1994).

[8] B.N.Engel, M.H.Wiedmann, R.A. Van Leeiwen, C.M.Falco, J.Appl. Phys. 75, 6401 (1994).

[9] T.Duden, E.Bauer, Phys. Rev. B 59, 468 (1999).

[10] K.Hyomi, A.Murayama, Y.Oka, U.Hiller, Ch.M.Falco, Appl. Phys. Lett. 80, 282 (2002).

[11] M.Kisielewski, A.Maziewski, M.Tekielak, A.Wawro, T.Baczewski, Phys.Rev.Let. 89, 8, 87203 (2002)

[12] M.Kisielewski, A.Maziewski, T.Polyakova and V.Zablotskii, Wide scale evolution of magnetization distribution in ultrathin films, praca wysłana do opublikowania.

[13] N.Spiridis, M.Kisielewski, A.Maziewski, T.lęzak, P.Cyganik, J.Korecki, Surface Science 507-510, 546 (2002).

[14] A.Wawro, L.T.Baczewski, P.Pankowski, M.Kisielewski, J.Sveklo, and A.Maziewski, Thin Solid Films 412, 34 (2002)

[15] M.Kisielewski, A.Maziewski, Z.Kurant, M.Tekielak, A.Wawro, L.T.Baczewski, J.Appl.Phys. 93, 7628 (2003).

[16] M.Kisielewski, A.Maziewski, V.Zablotskii, T.Polyakova, J.M.Garcia, A.Wawro, L.T.Baczewski J.Appl.Phys. 93, 6966 (2003)

[17] C.Chappert, H.Bernas, J.Ferré, V.Kottler, J.P.Jamet, Y.Chen, E.Cambril, T.Devolder, F.Rousseaux, Vmathet, H.Launois, Science, 280, 1919 (1998).

[18] S.P.Li, W.S.Lew, J.A.C.Bland, L.Lopez-Diaz, C.A.F.Vaz, M.Natali, Y.Chen, Phys.Rev.Letters, 88, 8, 87202 (2002).

[19] A.Wachowiak, J.Wiebe, M.Bode, O.Pietzsch, M.Morgenstern, R.Wiesendanger, Science 298, 577 (2002).

[20] M. Kisielewski, A. Maziewski, T. Polyakova, and V. Zablotskii, Models and simulations for analysis of domain sizes in ultrathin magnetic films, praca prezentowana na ICM 2003 w Rzymie, bedzie opublikowana w J.Magn.Magn.Mat. 2004.