Angular Momentum of an Electron
I think I can see how Bohr's idea of different energy levels sort of goes with Balmer's
formula, but I don't understand how angular momentum fits in.
Bohr knew that a photon's energy was equal to Planck's
constant times its frequency (this formula was discovered by Einstein during his work
on the photoelectric effect). If the Bohr model was
correct, he also knew that an emitted photon's energy was the same as the difference
between the upper and lower energy levels involved. So he had a relationship between the
energy levels and the frequencies of the photons...
But Balmer's formula specified the wavelength, not the frequency.
Ah, but don't forget that the two are related. The speed of a wave is equal to the product
of its wavelength and its frequency, as I was telling Kyla
earlier. A photon, or burst of
electromagnetic radiation, travels at the speed of light, c.
|
|
|
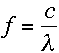
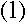
Quite so--and since we know that
|
|
|
|
|
|
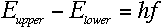
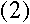
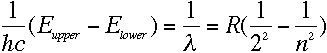
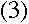
from Balmer's formula. Now, we can write the energy levels in
terms of the kinetic and potential energy of the electrons:
|
|
|
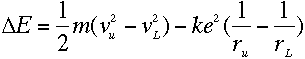
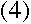
where m is the electron's mass, and v and r are its speed and orbital
radius at the upper and lower levels.
I'm beginning to see where angular momentum could go into this equation.
If the electron is in a circular orbit, then
|
|
|
|
|
|
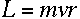
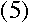
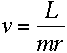
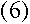
right?
Absolutely. Thus you can now write everything in terms of r and
L:
|
|
|
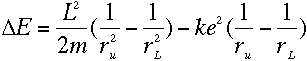
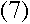
To find out what r is, we can apply Newton's second law, F=ma, to the
electron. The force on the electron can be found using Coulomb's Law:
|
|
|
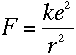
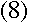
If the electron is in uniform circular motion, its acceleration is
|
|
|
|
|
|
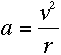
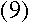
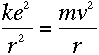
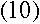
Substituting the value for v you obtained in equation (6)
and solving for r, we find that
|
|
|
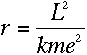
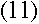
With everything in terms of L, we get the rather nice equation
|
|
|
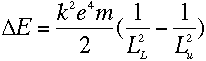
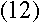
which means, from equation (3), that
|
|
|
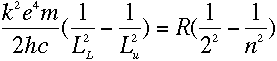
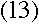
The two sides of that equation look really similar. Inside the parentheses, both sides have
1 over something squared minus 1 over something else squared, and all that stuff outside
the parentheses on the left is just a constant. So we should be able to pick some value of
L that would make the two sides be exactly the same...
That's just what Bohr did. It seemed logical to assume that the
squared terms on the right were related to his idea of energy levels. He associated each
energy level with an integer--called, originally enough, n--with n=1
corresponding to the ground state (the lowest possible energy level). Then the 2 and the
n in the Balmer series could represent electrons falling from the nth level
into the second...
I get it--so the 656 nm line would be produced by an electron falling from the third
energy level into the second, and so on. And then the
Lyman series would come from electrons falling into the first energy level, and in
the Paschen series they'd be falling into the third
--this makes so much sense!
| |
|
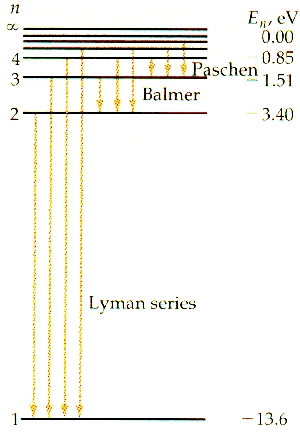
Doesn't it? Bohr realized that everything would work out beautifully
if he just assumed that the electron's angular momentum in the nth level was equal
to n times some constant. To find the constant, all he had to do was find the value
that makes equation (13) true. It turns out that the one
that works is
|
|
|
|
|
|
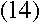
If you plug in the values of all those fundamental constants--the speed of light, the
electron's charge and mass, and so on--you will end up with just the value of the
