Czy można zmusić Arduino do wyświetlania grafiki 3D? Wiadomo, że do grania w gry potrzebujemy potężnych akceleratorów graficznych (karty nVidii lub ATI) lub dla mniej wymagającej grafiki mocnego CPU. Arduino może i nie ma wielkich zasobów mocy obliczeniowej, ale przy użyciu prostego wyświetlacza i lekkiej imitacji biblioteki 3d możemy uzyskać interesujące efekty. Stworzę “silnik 3D” – który w zasadzie jest tylko prostym rzutowaniem punktów na ekran. Pomimo ograniczonej funkcjonalności, możemy uzyskać ciekawe efekty takie jak obracająca się przestrzenna siatka sześcianu.

Cała sztuczka uzyskania wrażenia 3D polega na dobrym rzutowaniu punków w przestrzeni na piksele ekranu. Wiadomo, że obiekty dalsze są mniejsze, a te bliższe – są większe (perspektywa!). Ta obserwacja prowadzi mnie do banalnego pomysłu – nie będę rzutować trójwymiarowych punktów (x,y,z) na ekranik wyświetlacza (x,y), uwzględniając pozycję kamery w przestrzeni a jedynie… będę zmniejszać/zwiększać obiekty w zależności od ich odległości! Do oddania efektu głębi użyję funkcji wykładniczej a nie liniowej – to kolejna obserwacja, z którą trudno się nie zgodzić (obiekt dwa razy dalej nie jest wcale dwa razy mniejszy!). Dzięki temu obiekty znajdujące się bliżej będą powiększane, a te dalej pomniejszane.
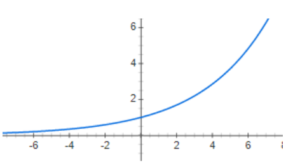
Daje nam to wrażenie, że obiekty znajdujące się dalej zbliżają lub oddalają się wolniej, a natomiast te bliżej – szybciej. Oddalające się punkty powinny się zbiegać do środka ekranu aby otrzymać efekt perspektywy punktowej.

Jako przykład użyjemy wyświetlacza Nokii 5110 oraz bibliotek Adafruit_PCD8544.h oraz Adafruit_GFX.h. Biblioteki posłużą nam do kontrolowania ekranem i wyświetlania linii.
Na początku musimy zaimplementować rzutowanie:
struct point2D{
int x,y;
};
struct point3D{
float x,y,z;
point2D CastTo2D(){
point2D ret;
ret.x = szerokosc_ekranu/2 + (x * X_SCALE * pow(Z_SCALE, z));
ret.y = wysokosc_ekranu/2 - (y * Y_SCALE * pow(Z_SCALE, z));
return ret;
}
};
Tworzę w ten sposób dwie struktury oraz metodę do późniejszego rzutowania na ekran. X_SCALE, Y_SCALE to współczynnki skalowania na poszczególnych osiach ekranu (bardzo przydatne w przypadku gdy piksele wyświetlacza nie są kwadratowe). Z_SCALE natomiast to współczynnik skalowania głębi.
Po podłączeniu ekranu do Arduino używamy bibliotek, żeby coś wyświetlić:
#include <SPI.h>
#include <Adafruit_GFX.h>
#include <Adafruit_PCD8544.h>
Adafruit_PCD8544 disp = Adafruit_PCD8544(5, 4, 3);
void setup() {
disp.begin();
disp.display(); // wyswietlanie buffera
}
Ten krótki kawałek kodu powinien wyświetlić logo Adafruit na ekranie. Można poświęcić chwilę na przyjrzenie się bliżej bibliotece i postarać się stworzyć własne logo, np. takie:

Gdy już wszystko nam działa możemy przejść do wyświetlenia czegoś przestrzennego. Pomocna będzie funkcja rysująca linię na ekranie pomiędzy punktami w przestrzeni:
void draw3DLine(point3D a, point3D b){
disp.drawLine(a.CastTo2D().x, a.CastTo2D().y, b.CastTo2D().x, b.CastTo2D().y, BLACK);
}
Musimy jednak mieć na uwadze w jaki sposób punkty przestrzenne są konwertowane na piksele ekranu. Punkt (0,0,0) znajduje się na środku ekranu, a składowa Z określa powiększenie (Z>0) lub pomniejszenie (Z<0) obiektu. Dla Z=0 rozmiar obiektu nie zostanie zmodyfikowany. Znaczenie ma również skala (X_SCALE, Y_SCALE), gdyż to właśnie przez te wartości mnożymy położenie punktu (dla małej skali musimy podać większe współrzędne, bo nasz obiekt na ekranie może okazać się jedynie małą kropką).
Wyświetlenie siatki sześcianu to odpowiednie połączenie ośmiu punktów – dosyć proste. Ale jak sprawić, żeby ten sześcian się obracał? W tym celu sięgamy po parę funkcji trygonometrycznych, a mianowicie sinus i cosinus.
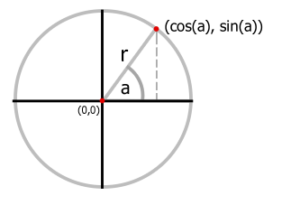
Zamiast podawać konkretne współrzędne x i y, możemy użyć kąta i odległości od środka. Punkt (r*cos(a), r*sin(a)), niezależnie od kąta a, jest zawsze oddalony o odległość r od punktu(0,0). Zwiększając ten kąt, punkt będzie “wędrować” po okręgu. Możemy to wykorzystać właśnie do obracania sześcianem.
Teraz możemy określić pionową parę punktów współrzędnymi:
(cos(a)*R, y, sin(a)*R) i (cos(a)*R, -y, sin(a)*R),
gdzie R to promień okręgu, po którym będą poruszać się punkty i jednocześnie połowa przekątnej sześcianu. Aby uzyskać następną parę punktów musimy je obrócić o 90 stopni, czyli do poprzedniego kąta dodajemy ℼ/2:
(cos(a+PI/2)*R, y, sin(a+PI/2)*R) i (cos(a+PI/2)*R, -y, sin(a+PI/2)*R).
W podobny sposób uzyskujemy pozostałe pary punktów dodając odpowiednio wielokrotność kąta ℼ/2 (dla trzeciej pary: 2*PI/2 i czwartej: 3*PI/2).
Kiedy już zapisaliśmy pozycje punktów w tej postaci, możemy zwiększać kąt a (lub zmniejszać co spowoduje obrót w przeciwnym kierunku). Warto pamiętać, że jest to kąt w radianach i należy go zwiększać o stosunkowo małe wartości.
Efekt jest następujący:
Kod programu:
#include <SPI.h>
#include <Adafruit_GFX.h>
#include <Adafruit_PCD8544.h>
#define Z_SCALE 1.2
#define X_SCALE 20
#define Y_SCALE 16
#define ANGLE 0.08
#define DT 60
#define RADIUS 1.3
struct point2D{
int x,y;
};
struct point3D{
float x,y,z;
point2D CastTo2D(){
point2D ret;
ret.x = round(42. + (x * X_SCALE * pow(Z_SCALE, z)));
ret.y = round(24. - (y * Y_SCALE * pow(Z_SCALE, z)));
return ret;
}
};
// Software SPI (slower updates, more flexible pin options)
// pin 7 - Serial clock out (SCLK)
// pin 6 - Serial data out (DIN)
// pin 5 - Data/Command select (D/C)
// pin 4 - LCD chip select (CS)
// pin 3 - LCD reset (RST)
Adafruit_PCD8544 disp = Adafruit_PCD8544(7, 6, 5, 4, 3);
void draw3DLine(point3D a, point3D b){
disp.drawLine(a.CastTo2D().x, a.CastTo2D().y, b.CastTo2D().x, b.CastTo2D().y, BLACK);
}
void setup() {
disp.begin();
}
float fi = 0.;
void loop() {
fi+=ANGLE;
disp.clearDisplay();
for(int i=0; i<4; i++){
point3D a= {cos(i*2*M_PI/4 + fi)*RADIUS, 1, sin(i*2*M_PI/4+ fi)*RADIUS};
point3D b= {cos(i*2*M_PI/4 + fi)*RADIUS, -1, sin(i*2*M_PI/4+ fi)*RADIUS};
draw3DLine(a,b);
point3D c= {cos((i+1)*2*M_PI/4 + fi)*RADIUS, 1, sin((i+1)*2*M_PI/4+ fi)*RADIUS};
point3D d= {cos((i+1)*2*M_PI/4 + fi)*RADIUS, -1, sin((i+1)*2*M_PI/4+ fi)*RADIUS};
draw3DLine(a,c);
draw3DLine(b,d);
}
disp.display();
delay(DT);
}
(c) Bartosz Bytler 2019
